Logic and logical operations
Logic has been used as a formal and unambiguous way to investigate thought, mind and knowledge for over two thousand years. The idea is that our thoughts are symbols, and thinking equates to performing operations upon these symbols (info here). I'm going to skip over most of the explanation of this - there are plenty of places to read about it on the net, but what we do need to know is about the three logical operators: AND, OR, and NOT. We'll also have a look at the exclusive OR operator - XOR.
I'll talk a little at the bottom of the page about the relevance of examining these functions in neurons.
I'll talk a little at the bottom of the page about the relevance of examining these functions in neurons.
|
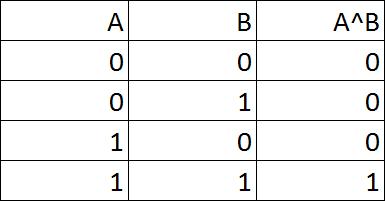
B represents another piece of information, such as "the cat is purring". The AND operator, often written as ^, is true only when both pieces of information is true, as shown in the third column of the truth table on the right. When A^B = 1, this means both "the cat is on the chair" and "the cat is purring". If either one, or both, of the propositions is false, the conjunction of the two will also be false. |
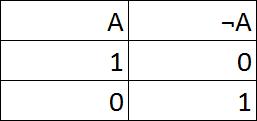
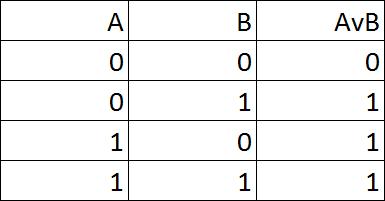
A represents a piece of information, such as "the cat is on the chair".
The NOT operator simply negates the information, so NOT(A) = "the cat is not on the chair". The operator is often written as ¬, so it will look like: ¬A. When A is true (value 1), ¬A is false (value 0), as can be seen in the truth table. Likewise, when A = 0, ¬A = 1. Finally, the OR operator, often written as v, is true when either one or both of the propositions is true. So, if the cat is on the chair, or it's purring, or if it's on the chair and purring, AvB will be true. This is shown in the truth table to the left. |
Neuron implementations
In 1943 neuroscientist Warren McCulloch and logician Walter Pitts published a paper showing how neurons could implement the three logical functions. The neurons they used were simple threshold neurons (which they named perceptrons).
And
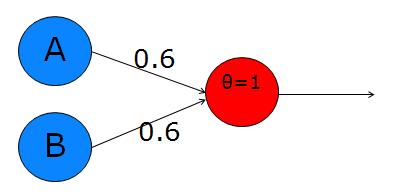
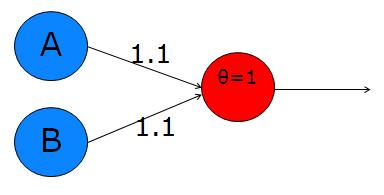
Let's start with the AND operator. Looking back at the logic table for the A^B, we can see that we only want the neuron to output a 1 when both inputs are activated. To do this, we want the sum of both inputs to be greater than the threshold, but each input alone must be lower than the threshold. Let's use a threshold of 1 (simple and convenient!). So, now we need to choose the weights according to the constraints I've just explained - how about 0.6 and 0.6? With these weights, individual activation of either input A or B will not exceed the threshold, while the sum of the two will be 1.2, which exceeds the threshold and causes the neuron to fire. Here is a diagram:
I've used a greek letter theta to denote the threshold, which is quite common practice. A and B are the two inputs. You can think of them as input neurons, like photoreceptors, taste buds, olfactory receptors, etc. They will each be set to 1 or 0 depending upon the truth of their proposition. The red neuron is our decision neuron. If the sum of the synapse-weighted inputs is greater than the threshold, this will output a 1, otherwise it will output a 0.
So, to test it by hand, we can try setting A and B to the different values in the truth table and seeing if the decision neuron's output matches the A^B column:
We have designed a neuron which implements a logical AND gate.
This is easy to implement in Excel. In fact, it's exactly the same as the neuron we created in What does a neuron do. Below there's a video that takes you through it quickly. Bear in mind that while the diagram drawn above flows from left to right, the neuron made in Excel flows down the page.
So, to test it by hand, we can try setting A and B to the different values in the truth table and seeing if the decision neuron's output matches the A^B column:
- If A=0 & B=0 --> 0*0.6 + 0*0.6 = 0. This is not greater than the threshold of 1, so the output = 0. Good!
- If A=0 & B=1 --> 0*0.6 + 1*0.6 = 0.6. This is not greater than the threshold, so the output = 0. Good.
- If A=1 & B=0 --> exactly the same as above. Good.
- If A=1 & B=1 --> 1*0.6 + 1*0.6 = 1.2. This exceeds the threshold, so the output = 1. Good.
We have designed a neuron which implements a logical AND gate.
This is easy to implement in Excel. In fact, it's exactly the same as the neuron we created in What does a neuron do. Below there's a video that takes you through it quickly. Bear in mind that while the diagram drawn above flows from left to right, the neuron made in Excel flows down the page.
or
|
Next up is the OR gate. Look back at the logic table. In this case, we want the output to be 1 when either or both of the inputs, A and B, are active, but 0 when both of the inputs are 0.
This is simple enough. If we make each synapse greater than the threshold, then it'll fire whenever there is any activity in either or both of A and B. This is shown on the right. Synaptic values of 1.1 are sufficient to surpass the threshold of 1 whenever their respective input is active. |
Updating the Excel file to change it from an AND gate to an OR gate is simple - just change the two synapse strengths! Check that it works by changing the inputs and making sure the output is as expected, as in the truth table.
not
|
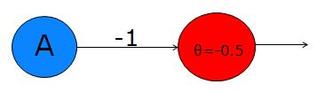
The decision neuron shown above, with threshold -0.5 and synapse weight -1, will reverse the input:
A = 1 --> output = 0 A = 0 --> ouput = 1 |
The last one we talked about above was the NOT gate. This is a little tricky. We have to change a 1 to a 0 - this is easy, just make sure that the input doesn't exceed the threshold. However, we also have to change a 0 to a 1 - how can we do this? The answer is to think of our decision neuron as a tonic neuron - one whose natural state is active. To make this, all we do is set the threshold lower than 0, so even when it receives no input, it still exceeds the threshold. In fact, we have to set the synapse to a negative number (I've used -1) and the threshold to some number between that and 0 (I've used -0.5).
|
Here's a video showing how to make the NOT gate neuron in Excel:
XOR
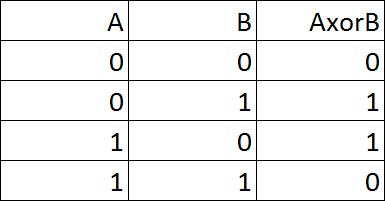
As I mentioned at the top, there is also something called the XOR (exclusive OR) operator. This actually put a spanner in the works of neural network research for a long time because it is not possible to create an XOR gate with a single neuron, or even a single layer of neurons - you need to have two layers. First of all, let's have a look at it's truth table.
|
Exclusive OR means that we want a truth value of 1 either when A is 1, or when B is 1, but not when both A and B are 1. The truth table on the right shows this.
To use a real world example, in the question "would you like tea or coffee?", the "or" is actually and exclusive or, because the person is offering you one or the other, but not both. Contrast this with "would you like milk or sugar?". In this case you can have milk, or sugar, or both. |
As I said, it is not possible to set up a single neuron to perform the XOR operation (more details on a later page). This is where networks come into it. The only way to solve this problem is to have a bunch of neurons working together. But we can use what we have learnt from the other logic gates to help us design this network.
I'll start by breaking down the XOR operation into a number of simpler logical functions:
A xor B = (AvB) ^ ¬(A^B)
All that this says is that A xor B is the same as A or B and not A and B. In other words, it is the same truth table as AvB, but with the A^B line (the bottom line, when both inputs are 1) removed (or set to 0).
This line of logic contains three important operations: an OR operator in the brackets on the left, an AND operator in the brackets on the right, and another AND operator in the middle.
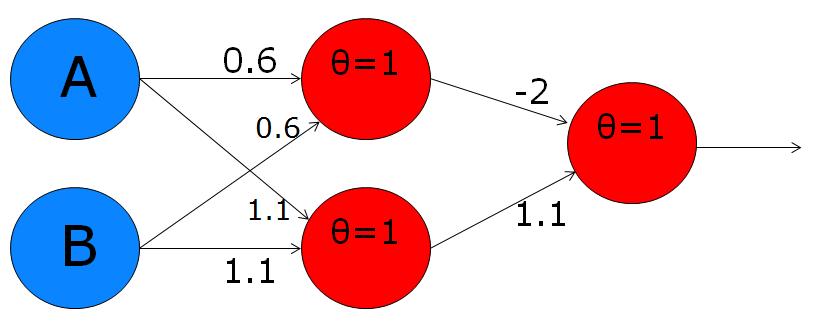
We can create a neuron for each of these operations, and stick them together like this:
I'll start by breaking down the XOR operation into a number of simpler logical functions:
A xor B = (AvB) ^ ¬(A^B)
All that this says is that A xor B is the same as A or B and not A and B. In other words, it is the same truth table as AvB, but with the A^B line (the bottom line, when both inputs are 1) removed (or set to 0).
This line of logic contains three important operations: an OR operator in the brackets on the left, an AND operator in the brackets on the right, and another AND operator in the middle.
We can create a neuron for each of these operations, and stick them together like this:
The upper of the two red neurons in the first layer has two inputs with synaptic weights of 0.6 each and a threshold of 1, exactly the same as the AND gate we made earlier. This is the AND function in the brackets on the right of the formula I wrote earlier. Notice that it is connected to the output neuron with a negative synaptic weight (-2). This accounts for the NOT operator that precedes the brackets on the right hand side.
The lower of the two red neurons in the first layer has two synaptic weights of 1.1 and a threshold of 1, just like the OR gate we made earlier. This neuron is doing the job of the OR operator in the brackets on the left of the formula.
The output neuron is performing another AND operation - the one in the middle of the formula. Practically, this output neuron is active whenever one of the inputs, A or B is on, but it is overpowered by the inhibition of the upper neuron in cases when both A and B are on.
Here's a video of me making this network:
The lower of the two red neurons in the first layer has two synaptic weights of 1.1 and a threshold of 1, just like the OR gate we made earlier. This neuron is doing the job of the OR operator in the brackets on the left of the formula.
The output neuron is performing another AND operation - the one in the middle of the formula. Practically, this output neuron is active whenever one of the inputs, A or B is on, but it is overpowered by the inhibition of the upper neuron in cases when both A and B are on.
Here's a video of me making this network:
Relevance
So what is the point in implementing the AND, OR, NOT and XOR logic operators in artificial neurons?
I mentioned at the beginning that logic was developed as a model of how our mind works - our concepts of things are the symbols, and the process of thinking is manipulation of these symbols. So, logic was invented as a model of the mind, and the logical operators that we looked at were discovered to be all that is needed (more or less) to manipulate the symbols in the ways we seem to do. It is then very reassuring that we can show that neurons are capable of implementing these operators. Moreover, the fact that over 2000 years of development has gone into logic, and there is a good understanding of how quite complex ideas can be broken down into simpler units (the basic symbols), so by showing that neurons can do the same operations, we justify the use of this massive body of knowledge. This is why McCulloch and Pitts' looked to logic when trying to understand how the complex behaviours of the brain could be produced by simple cells wired together in different ways.
The next reason is that it is useful (and interesting) to know what, exactly, different configurations of neurons can do. McCulloch and Pitts originally showed a wide range of logical operators that could be implemented by neurons, but, as we saw above, the XOR cannot be implemented in a network consisting of just a single layer of neurons. This task is too complicated, and requires a multi-layer network. Further research showed that even the most complicated of problems could be solved by a network with two layers, like the XOR network on this page (but with more neurons in each layer). So there is no need for more than two layers of neurons if we only focus on whether or not the problem can be solved by the network (not speed, flexibility, etc). This leads to the question of why our brains tend to have six layers in the neocortex. What are the other layers doing? This is a good example of how modelling and theoretical neuroscience can contribute to the study of the nervous system by pointing out which questions are relevant for a functional understanding of what's going on.
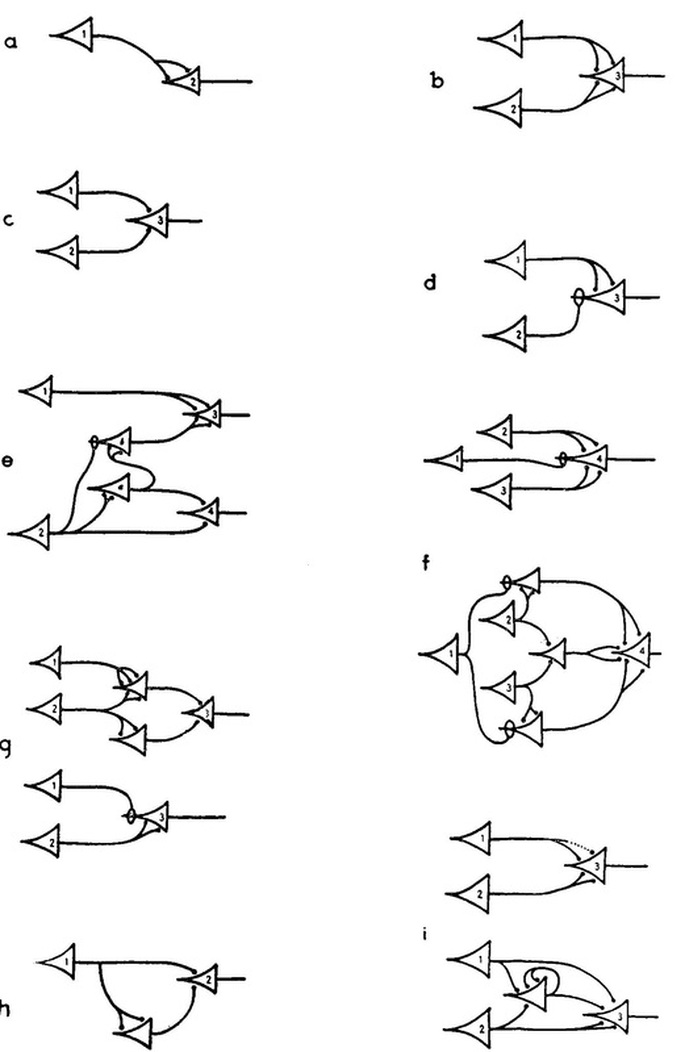
As a little challenge for you, here are the configurations presented in the McCulloch and Pitts paper. Why don't you try implementing them yourself and exploring their behaviours? The numbers in the cell bodies are the thresholds of the respective neurons.
I mentioned at the beginning that logic was developed as a model of how our mind works - our concepts of things are the symbols, and the process of thinking is manipulation of these symbols. So, logic was invented as a model of the mind, and the logical operators that we looked at were discovered to be all that is needed (more or less) to manipulate the symbols in the ways we seem to do. It is then very reassuring that we can show that neurons are capable of implementing these operators. Moreover, the fact that over 2000 years of development has gone into logic, and there is a good understanding of how quite complex ideas can be broken down into simpler units (the basic symbols), so by showing that neurons can do the same operations, we justify the use of this massive body of knowledge. This is why McCulloch and Pitts' looked to logic when trying to understand how the complex behaviours of the brain could be produced by simple cells wired together in different ways.
The next reason is that it is useful (and interesting) to know what, exactly, different configurations of neurons can do. McCulloch and Pitts originally showed a wide range of logical operators that could be implemented by neurons, but, as we saw above, the XOR cannot be implemented in a network consisting of just a single layer of neurons. This task is too complicated, and requires a multi-layer network. Further research showed that even the most complicated of problems could be solved by a network with two layers, like the XOR network on this page (but with more neurons in each layer). So there is no need for more than two layers of neurons if we only focus on whether or not the problem can be solved by the network (not speed, flexibility, etc). This leads to the question of why our brains tend to have six layers in the neocortex. What are the other layers doing? This is a good example of how modelling and theoretical neuroscience can contribute to the study of the nervous system by pointing out which questions are relevant for a functional understanding of what's going on.
As a little challenge for you, here are the configurations presented in the McCulloch and Pitts paper. Why don't you try implementing them yourself and exploring their behaviours? The numbers in the cell bodies are the thresholds of the respective neurons.
The original paper is here.
And if all of this seems a little far removed from biology, it actually seems like the hierarchy of processing areas that visual (and other) information travels through in the brain are organised in chains of AND and OR gates. First the AND neurons search for co-active patterns of activation, then the OR neurons fire to signal if a pattern has been sensed anywhere in their receptive field, according to whether any of the AND gates presynaptic to them are active. I have build a model of this form on my Neurons fire & ideas emerge page.
And if all of this seems a little far removed from biology, it actually seems like the hierarchy of processing areas that visual (and other) information travels through in the brain are organised in chains of AND and OR gates. First the AND neurons search for co-active patterns of activation, then the OR neurons fire to signal if a pattern has been sensed anywhere in their receptive field, according to whether any of the AND gates presynaptic to them are active. I have build a model of this form on my Neurons fire & ideas emerge page.