what does a neuron do?
Here we're going to look at what a single neuron does. We know they receive and send messages from and to the environment (sensory neurons and motor neurons) and between one another, but how does their manipulation of the information they carry cause the behaviours, thoughts and feelings we have? Is there a way we can abstract away from the synapses, dendrites, neurotransmitters, ion channels, etc, and focus instead on function to gain a better understanding of the job the neurons are performing?
To explore these question, we'll make a model of the simplest neuron we can imagine: a two input one output neuron
To explore these question, we'll make a model of the simplest neuron we can imagine: a two input one output neuron
AN ARTIFICIAL NEURON (A PERCEPTRON)
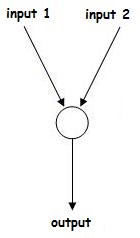
To explore these question, we'll make a model of the simplest neuron we can imagine: a two input one output neuron like the one on the left.
To help with conceptualisation, let's create a scenario. This is the neuron in our brain that decides whether we eat or don't or don't eat a piece of food that is in front of us based upon the food's albedo (whiteness) and how sweet it smells. Input 1 is connected to an albedo sensor which is active with a value of 1 if the food is white and with an activation of 0 if the food is dark. Input 2 is connected to a sweetness sensor which is active with a value of 1 when the food smells sweet, and with a value of 0 when it doesn't. The output is a motor command to eat the food or not, taking a value of 1 or 0 respectively.
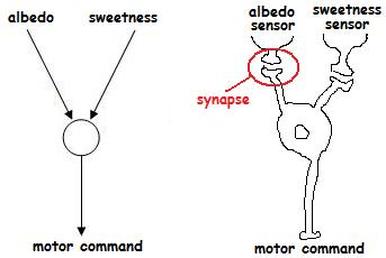
Here's a little picture of how our artificial neuron could be realised as a biological neuron. The important thing that I want to show here is that the two sensors are not actually a part of our neuron, but are connected to it via synapses. The albedo and sweetness are actually features of the environment (the food, in this case), so they can change from moment to moment as we look at different foods.
The synapses are where the main information processing work of the neuron occurs because they can amplify or attenuate the signal from either sensor in order to make the neuron more or less sensitive to either albedo or sweetness. In an artificial neuron, the synapses are usually called weights because they determine how "heavy" the contribution of their input is to the post-synaptic neuron's activity.
The synapses are where the main information processing work of the neuron occurs because they can amplify or attenuate the signal from either sensor in order to make the neuron more or less sensitive to either albedo or sweetness. In an artificial neuron, the synapses are usually called weights because they determine how "heavy" the contribution of their input is to the post-synaptic neuron's activity.
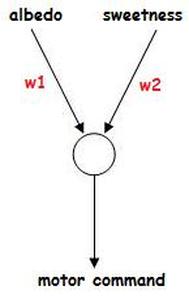
In our artificial neuron, the weights (synapses) are represented by the two lines coming into the cell body. In this picture I've labelled the two weights w1 and w2. When we actually build the model, these will be numbers. The stronger the synapse, the bigger the number.
Biological neurons can be excitatory (glutaminergic) or inhibitory (GABAergic). Actually, it's the receptors in the synapse that determines this, and, correspondingly, our weight may also be either excitatory (a positive number) or inhibitory (a negative number). So...
Biological neurons can be excitatory (glutaminergic) or inhibitory (GABAergic). Actually, it's the receptors in the synapse that determines this, and, correspondingly, our weight may also be either excitatory (a positive number) or inhibitory (a negative number). So...
- a weight of 10 means the pre-synaptic neuron has a stronger excitatory effect upon the neuron than a weight of 5.
- a weight of -1 inhibits the post-synaptic neuron.
- a weight of 0 means the pre-synaptic neuron or sensor has no effect at all on the post-synaptic neuron.
The next thing we need to look at is the cell body itself. Each of the different inputs passes a weighted message to the cell body. What happens next? It's pretty simple: we just add together all of the weighted inputs to get the cell's activation. So, with two inputs, we get this little equation:
activation = (input1 * w1) + (input2 * w2)
But the cell body has not yet finished its work. The output of the neuron is all or nothing, which we can represent as a 1 or a 0. However, the activation that we've just defined as the sum of weighted inputs could be of any value at all (0.3 or 55.5, for example). So we need to determine a way of transforming the activation into a binary output. This is also easy, and it's called the threshold function. If the activation exceeds a certain threshold that we determine (2, for example), the neuron fires (outputs a 1). Otherwise, it doesn't fire (outputs a 0).
And that's the neuron fully defined. There's still one more thing to discuss before we make the program though - the inputs. What are the different foods we are going to be presented with? Well, we have two binary inputs, which gives us four possible combinations: (0 0) (0 1) (1 0) (1 1)
This means there are a maximum of four distinct things that our neuron will be able to recognise (it would be more if we had more inputs, but let's keep it simple). Since we are using the metaphor of a food recognising neuron, we can choose four foods quite arbitrarily.
activation = (input1 * w1) + (input2 * w2)
But the cell body has not yet finished its work. The output of the neuron is all or nothing, which we can represent as a 1 or a 0. However, the activation that we've just defined as the sum of weighted inputs could be of any value at all (0.3 or 55.5, for example). So we need to determine a way of transforming the activation into a binary output. This is also easy, and it's called the threshold function. If the activation exceeds a certain threshold that we determine (2, for example), the neuron fires (outputs a 1). Otherwise, it doesn't fire (outputs a 0).
And that's the neuron fully defined. There's still one more thing to discuss before we make the program though - the inputs. What are the different foods we are going to be presented with? Well, we have two binary inputs, which gives us four possible combinations: (0 0) (0 1) (1 0) (1 1)
This means there are a maximum of four distinct things that our neuron will be able to recognise (it would be more if we had more inputs, but let's keep it simple). Since we are using the metaphor of a food recognising neuron, we can choose four foods quite arbitrarily.
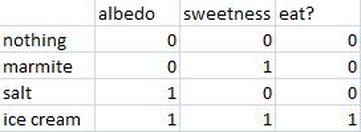
I've chosen four foods that more or less fit the albedo and sweetness constraints that we have.
The first option is when we are looking at nothing, which has neither albedo nor sweetness.
Does Marmite smell sweet? I try to avoid smelling it! But, for our purposes, I've put it as having a sweet smell, but no whiteness.
You can work out the other two.
The other thing we can see from this table is the desired output of our neuron. I've also decided this arbitrarily. This neuron is probably situated in my head, cos the only thing from this list that I'd like to eat is the ice cream.
The first option is when we are looking at nothing, which has neither albedo nor sweetness.
Does Marmite smell sweet? I try to avoid smelling it! But, for our purposes, I've put it as having a sweet smell, but no whiteness.
You can work out the other two.
The other thing we can see from this table is the desired output of our neuron. I've also decided this arbitrarily. This neuron is probably situated in my head, cos the only thing from this list that I'd like to eat is the ice cream.
making it in excel ....
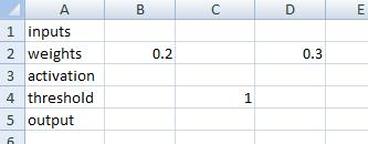
In Excel, type in what the same as I've done in the picture here.
Note that the inputs (cells B1 & D1) are empty. It's not looking at anything.
I've chosen the weights arbitrarily. You'll have a chance to explore what happens when different weights are used later.
The threshold has also been chosen arbitrarily. For now, use 1, but you'll see later that it's not so important what value you use as long as you select the weights appropriately.
Next step - we need to make the activation be the sum of weighted inputs, as we said above. The activation will be calculated in cell C3, so click on this cell and type the following:
=B1*B2 + D1*D2
Hit return, then check that it's worked by double clicking on C3. You should see a colour-coded sum of the cells that the equation is using. Be sure you know what each element of this equation actually means: B1 is the albedo value of the food that the neuron is looking at, etc.
And finally, we need to compare the activation to the threshold to see if the neuron should fire or not. This will happen in cell C5, so click on it. This time let's use a built-in Excel function. Go to the "Formulas" tabbed menu, then find the "Insert Function" button on the left. When you click this, a floating box will come up like the one shown below.
Note that the inputs (cells B1 & D1) are empty. It's not looking at anything.
I've chosen the weights arbitrarily. You'll have a chance to explore what happens when different weights are used later.
The threshold has also been chosen arbitrarily. For now, use 1, but you'll see later that it's not so important what value you use as long as you select the weights appropriately.
Next step - we need to make the activation be the sum of weighted inputs, as we said above. The activation will be calculated in cell C3, so click on this cell and type the following:
=B1*B2 + D1*D2
Hit return, then check that it's worked by double clicking on C3. You should see a colour-coded sum of the cells that the equation is using. Be sure you know what each element of this equation actually means: B1 is the albedo value of the food that the neuron is looking at, etc.
And finally, we need to compare the activation to the threshold to see if the neuron should fire or not. This will happen in cell C5, so click on it. This time let's use a built-in Excel function. Go to the "Formulas" tabbed menu, then find the "Insert Function" button on the left. When you click this, a floating box will come up like the one shown below.
Our logical test is whether or not the activation is greater than the threshold. Since we've put the activation in cell C3 and the threshold in cell C4, our formula for this is C3>=C4, meaning "if C3 is greater than or equal to C4". If this is the case, we want the neuron to fire, so we put 1 (fire) in the "Value_if_true" field and 0 (don't fire) in the "Value_if_false" field. Click ok.
Now the only thing that is missing is the inputs. Well, we can input these by hand. Just put the values for the thing you want to present to the neuron in the two inputs cells, B1 and D1 and observe whether the neuron fires or not from whether a 1 or a 0 appears in the output cell, C5.
Now the only thing that is missing is the inputs. Well, we can input these by hand. Just put the values for the thing you want to present to the neuron in the two inputs cells, B1 and D1 and observe whether the neuron fires or not from whether a 1 or a 0 appears in the output cell, C5.
playing with the neuron
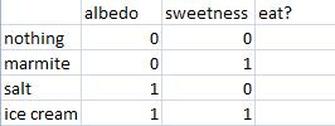
The test for our neuron is whether it will eat only the ice cream and none of the other things (by outputting a 1). Test it yourself.
Does this neuron behave correctly?
If it doesn't (and if you've used the same weights as I did, it won't!), then we need to change the weights.
Let's try weights of 1.5 for albedo and 1 for sweetness... in cell B2 put 1.5 and in cell D2 put 1.
- Show the neuron "nothing" by putting 0 in cell B1 (albedo sensor) and 0 in cell D1 (sweetness sensor). What does the neuron output? (remember that the desired behaviour is 0 - not to eat)
- Show the neuron "marmite" by putting 0 in B1 and 1 in D1. What does it output?
- Show the neuron "salt": 1 in B1 and 0 in D1.
- Show the neuron "ice cream": 1 in both input sensors. This is the only situation in which the neuron should decide to "eat". Does it output 1, as desired?
Does this neuron behave correctly?
If it doesn't (and if you've used the same weights as I did, it won't!), then we need to change the weights.
Let's try weights of 1.5 for albedo and 1 for sweetness... in cell B2 put 1.5 and in cell D2 put 1.
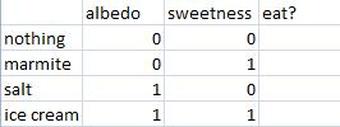
With the new weights, perform the tests again.
- For which foods does the neuron fire and not fire?
- Is this the desired behaviour?
Ok, you must be getting sick of entering 1s and 0s for the inputs now, so this time I'll give you some weights that will solve the problem: albedo = 0.6, sweetness = 0.7. A bit later we'll look at why these weights in particular work while the others didn't. You may be able to work it out for yourself. It's not so difficult.
sUMMARY
We've taken a look at how neurons process information. The focus has been on the function they perform rather than what they look like, what they are made of, what neurotransmitters they produce, where in the brain they are situated, etc.
Things you should take away from this:
The model that we have made is officially called a PERCEPTRON, but it's not a complete perceptron yet because it's not capable of learning. Go to my learning page to find out how to extend the model.
Things you should take away from this:
- A neuron takes all the information from any pre-synaptic neurons that it is connected to, adds it up, and either fires or not, depending on whether the summed activation is great enough.
- Synapses (weights) can be excitatory (+) or inhibitory (-).
- Synapses can amplify or attenuate the pre-synaptic message.
- The activation is transformed into the output.
- One neuron makes a binary decision: fire or don't fire. In other words, a neuron is able to categorise combinations of inputs into two groups.
The model that we have made is officially called a PERCEPTRON, but it's not a complete perceptron yet because it's not capable of learning. Go to my learning page to find out how to extend the model.